Python 넘파이 다항 회귀 예제 : np.polyfit 함수
파이썬에서 numpy 모듈의 polyfit 메소드를 활용하여 1차, 2차 및 n차 다항 회귀식을
구해보고, 결과를 시각화해보는 예시를 다루어보겠습니다.
1차 회귀식 구하기 및 결과 시각화 예시
먼저, 다음과 같은 x와 y에 대한 데이터가 있다고 가정해보겠습니다.
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 6, 8, 11, 19]
polyfit 함수의 사용법은 polyfit(x, y, 차수) 형태로 매우 간단하게 이용이 가능합니다.
예를 들어, 1차식으로 회귀를 진행한 결과는 아래와 같습니다.
import numpy as np
print(np.polyfit(x, y, 1))
# [ 3.31428571 -3.6 ] -> y = 3.314x - 3.6결과로는 차수 + 1만큼의 길이의 숫자 배열이 반환되는데,
이 숫자들은 n차식 계수부터 차례대로 1차식 내려가며 상수항의 계수까지를 의미합니다.
위의 결과에서는 회귀식으로 대략 y = 3.314x - 3.6 정도의 결과가 반환되었습니다.
이제 위에서 구한 회귀식을 바탕으로
실제 x와 y 값들의 좌표와 회귀선을 같이 시각화해보는 코드의 예시는 아래와 같습니다.
import matplotlib.pyplot as plt
poly = np.polyfit(x, y, 1) # 1차, 상수항 계수가 순서대로 들어있는 배열
y_pred = np.array(x) * poly[0] + poly[1] # x 값에 회귀를 진행한 예측 y 값
plt.plot(x, y_pred, color = 'b')
plt.scatter(x, y, color = 'r')
plt.show()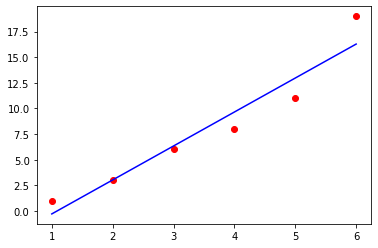
2차 회귀식 구하기 및 결과 시각화 예시
이번에는 2차 회귀를 진행한 결과를 살펴보고 시각화를 마찬가지로 진행해보겠습니다.
먼저, polyfit 함수로 2차 회귀식을 구한 결과는 다음과 같습니다.
print(np.polyfit(x, y, 2))
# [ 0.53571429 -0.43571429 1.4 ] -> y = 0.5357x^2 - 0.4357x + 1.4대략 y = 0.5357x^2 - 0.4357x + 1.4에 가까운 식으로 회귀가 진행되었습니다.
이번에는 위에서 구한 회귀식으로 시각화를 같은 식으로 해보겠습니다.
여기서 유의할 사항은 2차 이상의 식의 경우에는 np.linspace 함수를 이용하여
촘촘한 x 값을 새롭게 선언해준 뒤 이를 바탕으로 회귀 예측 식을 구해주셔야
회귀선이 완만한 곡선으로 그려질 수 있습니다.
poly = np.polyfit(x, y, 2) # 2차, 1차, 상수항 계수가 순서대로 들어있는 배열
x_line = np.linspace(1, 6, 100) # 곡선을 완만하게 그리기 위한 linspace 객체 선언
y_pred = x_line ** 2 * poly[0] + x_line * poly[1] + poly[2]
plt.plot(x_line, y_pred, color = 'b')
plt.scatter(x, y, color = 'r')
plt.show()
n차(n > 2) 회귀식 구하기 및 결과 시각화 예시
2차 이상의 고차 다항식으로 회귀식 추정 및 시각화를 진행하는 경우도
2차식의 예시와 마찬가지로 진행해주시면 됩니다.
5차식으로 회귀 진행 및 회귀선을 시각화를 해본 예시 코드는 아래와 같습니다.
여기서는 예측 값을 계산할 때, for문을 사용하여 각 차의 항들을 더해주었습니다.
poly = np.polyfit(x, y, 5) # 5, 4, 3, 2, 1차, 상수항 계수가 순서대로 들어있는 배열
x_line = np.linspace(1, 6, 100) # 곡선을 완만하게 그리기 위한 linspace 객체 선언
y_pred = np.zeros_like(x_line) # 예측 값을 구하기 위해 모든 값이 0인 배열 선언
for i in range(6): # 5, 4, 3, 2, 1차, 상수항에 대한 값들을 for문으로 더해서 계산
y_pred += x_line ** (5 - i) * poly[i]
plt.plot(x_line, y_pred, color = 'b')
plt.scatter(x, y, color = 'r')
plt.show()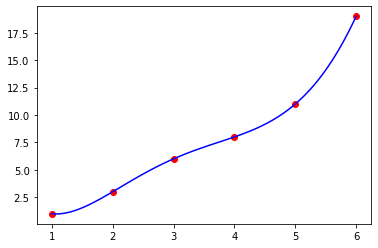
차수를 높이니 실제 x 및 y값의 위치에 매우 가깝게 회귀가 진행된 점을 살펴볼 수 있었습니다.
'Python > Numpy' 카테고리의 다른 글
| 파이썬에서 중복 없이 숫자 뽑기 / 리스트 랜덤 자료 추출 (0) | 2022.06.22 |
|---|---|
| [Numpy] 파이썬 삼각함수(sin, cos, tan)와 역삼각함수(arcsin, arccos, arctan) 메소드 정리 (0) | 2022.06.07 |
| [Numpy] 파이썬 단위행렬 함수 np.eye(), 역행렬 함수 LA.inv() (0) | 2022.05.15 |